CRC算法原理
CRC 算法的基本原理是将数据看作一个大数,与一个预定义的除数使用特殊的除法相除,所得的余数即为数据的 CRC 校验值。
生成多项式
算法的数学原理与多项式相关,用到的除法也基于多项式除法,预定义的除数也叫“生成多项式”,这里的多项式都是只有一个未知数并且各项系数只能是 0 或 1 的多项式
我们以CRC-4/ITU为例,其生成多项式是{x^4+x+1},也即:
1x^4+0x^3+0x^2+1x^1+1x^0
如果我们令 x=2,则多项式中每一项的系数可以看作一个二进制数的对应位,即 (10011)2(10011)2,是一个 5 位的二进制数,那么用它来做除数,最后可以得到 4 位的余数,也就是 CRC-4/ITU 中的 4。由此可见,生成多项式的首位必然是 1,在一般表示生成多项式的时候我们都省略最高位,再写成十六进制就是 0x03。
模二多项式除法
我们先看多项式乘法:
(x^4+x^1+x^0)×(x^4+x^3+x^0)=x^8+x^7+x^4+x^5+x^4+x^1+x^4+x^3+x^0
这里我们没有合并同类项,如果按照常规的方式合并同类项,即
x^8+x^7+x^5+3x^4+x^3+x^1+x^0
那就是普通的多项式乘法;对于 CRC 算法,加减法采用模二运算,也就是最后的系数除以 2 取余数,不产生进位,所以最后的结果是:
x^8+x^7+x^5+x^4+x^3+x^1+x^0^
这里的加减法采用模二运算后,实际上也就变成了我们平时说的异或(XOR/⊕⊕)运算,以上面x^4的系数为例:
1+1+1=3≡1(mod2)1+1+1=3≡1(mod2)
1⊕1⊕1=11⊕1⊕1=1
下面我们以字母 b 为例,来尝试计算其校验值:
1)b 的 ASCII 码 为 98,即 (1100010)2(1100010)2,并在其后追加 4 (生成多项式位数减1) 个 0,即 (11000100000)2(11000100000)2
2)做除法: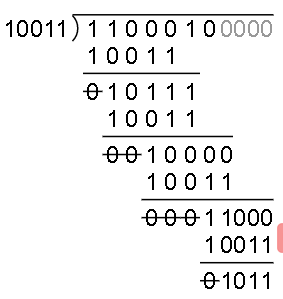
这里由于生成多项式的首位必然是 1,所以我们可以省略首位的 1,同时在计算的时候对每一步被除数首位的 1 直接忽略,那么简化后的除法如下: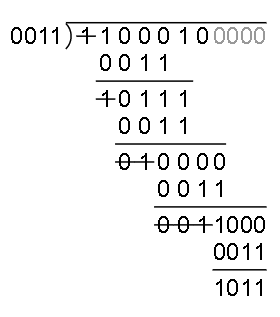
位反转
通过上面的计算,我们得到了余数 (1011)2(1011)2,但是这和我们使用其他工具计算的 b 的 CRC-4/ITU 校验值不相符,
原因是 CRC-4/ITU 的定义中还有两项操作,它要求输入数据在进行计算之前按字节进行位反转,并且最后的结果也要进行位反转,也即输入位反转及输出位反转。
还是以上面的b为例,其二进制为 (1100010)2(1100010)2,我们把首位省略的0补齐,即 (01100010)2(01100010)2,反转后为 (01000110)2(01000110)2,即字母F,也就是说我们上面其实是在计算F的 CRC-4/ITU 校验值,如果把最后的结果再反转一遍,应该 得到 (1101)2(1101)2。
我们再用其他工具计算 F 的 CRC-4/ITU 校验值,结果正是 (1101)2(1101)2
需要注意的是这里是按字节进行位反转,字节序本身是不变的。
初始值与输出异或值
除了上面的位反转的情况,实际应用中的 CRC 算法还有初始值和输出异或值,并且它们的最大位数为生成多项式位数减一,例如对于 CRC-4、CRC-8 分别为 4 、8,而上面的 CRC-4/ITU 我们可以看作这两个值都是 0。
在计算的时候,初始值要首先与数据的最高位对齐进行异或,然后在进行上述运算求得余数,如果算法要求输入位反转,则应在异或初始值之前反转。
最后的余数再与输出异或值进行异或,如果算法要求输出位反转,则也应该在异或运算之前反转。
完整示例
下面我们以 CRC-5/USB 为例,做一次完整的计算。CRC-5/USB 的生成多项式是 x5+x2+1x5+x2+1,十六进制表示为 0x05,二进制 (00101)2(00101)2 (均省略首位1), 初始值及输出异或值均为 0x1f,二进制 (11111)2(11111)2,并且算法要求输入及输出位反转。
假设要计算的数据是 2b (ASCII),两个字符其分别对应二进制 (00110010)2(00110010)2、(01100010)2(01100010)2。
1)位反转,得到数据 (0100110001000110)2(0100110001000110)2
2)补位(5个0),得到数据 (010011000100011000000)2(010011000100011000000)2
3)异或初始值 (11111)2(11111)2,得到数据 (101101000100011000000)2(101101000100011000000)2,注意这里是高位对齐
4)模二除法运算: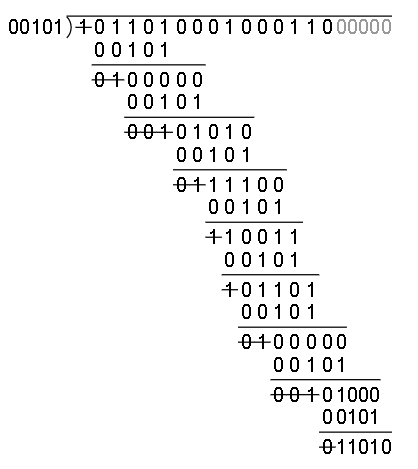
我们得到余数 (11010)2(11010)2,需要注意的是这里最后一行,如果我们划掉的是 1,那么我们还需要再做一次异或生成多项式的运算,总之运算结束的标志是所有原始数据位都被划掉了。
5)对余数进行位反转,得到 (01011)2(01011)2
6)与输出异或值 (11111)2(11111)2 进行异或,得到 (10100)2(10100)2
这与我们使用其他工具计算所得的结果相符。